Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series. They are named for the parity of the powers of the power functions which satisfy each condition: the function f(x) = xn is an even function if n is an even integer, and it is an odd function if n is an odd integer.
Contents |
Even functions
Let f(x) be a real-valued function of a real variable. Then f is even if the following equation holds for all x in the domain of f:
Geometrically speaking, the graph face of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis.
Examples of even functions are |x|, x2, x4, cos(x), and cosh(x).
Odd functions
Again, let f(x) be a real-valued function of a real variable. Then f is odd if the following equation holds for all x in the domain of f:
or
Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin.
Examples of odd functions are x, x3, sin(x), sinh(x), and erf(x).
Some facts
A function's being odd or even does not imply differentiability, or even continuity. For example, the Dirichlet function is even, but is nowhere continuous. Properties involving Fourier series, Taylor series, derivatives and so on may only be used when they can be assumed to exist.
Basic properties
- The only function which is both even and odd is the constant function which is equal to zero (i.e., f(x) = 0 for all x).
- The sum of an even and odd function is neither even nor odd, unless one of the functions is equal to zero over the given domain.
- The sum of two even functions is even, and any constant multiple of an even function is even.
- The sum of two odd functions is odd, and any constant multiple of an odd function is odd.
- The product of two even functions is an even function.
- The product of two odd functions is an even function.
- The product of an even function and an odd function is an odd function.
- The quotient of two even functions is an even function.
- The quotient of two odd functions is an even function.
- The quotient of an even function and an odd function is an odd function.
- The derivative of an even function is odd.
- The derivative of an odd function is even.
- The composition of two even functions is even, and the composition of two odd functions is odd.
- The composition of an even function and an odd function is even.
- The composition of any function with an even function is even (but not vice versa).
- The integral of an odd function from −A to +A is zero (where A is finite, and the function has no vertical asymptotes between −A and A).
- The integral of an even function from −A to +A is twice the integral from 0 to +A (where A is finite, and the function has no vertical asymptotes between −A and A).
Series
- The Maclaurin series of an even function includes only even powers.
- The Maclaurin series of an odd function includes only odd powers.
- The Fourier series of a periodic even function includes only cosine terms.
- The Fourier series of a periodic odd function includes only sine terms.
Algebraic structure
- Any linear combination of even functions is even, and the even functions form a vector space over the reals. Similarly, any linear combination of odd functions is odd, and the odd functions also form a vector space over the reals. In fact, the vector space of all real-valued functions is the direct sum of the subspaces of even and odd functions. In other words, every function f(x) can be written uniquely as the sum of an even function and an odd function:
-
- where
- is even and
- is odd. For example, if f is exp, then fe is cosh and fo is sinh.
- The even functions form a commutative algebra over the reals. However, the odd functions do not form an algebra over the reals.
Harmonics
In signal processing, harmonic distortion occurs when a sine wave signal is sent through a memoryless nonlinear system, that is, a system whose output at time  only depends on the input at time
only depends on the input at time  and does not depend on the input at any previous times. Such a system is described by a response function
and does not depend on the input at any previous times. Such a system is described by a response function 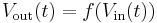 . The type of harmonics produced depend on the response function
. The type of harmonics produced depend on the response function  :[1]
:[1]
- When the response function is even, the resulting signal will consist of only even harmonics of the input sine wave;
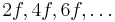
- The fundamental is also an odd harmonic, so will not be present.
- A simple example is a full-wave rectifier.
- When it is odd, the resulting signal will consist of only odd harmonics of the input sine wave;
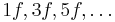
- The output signal will be half-wave symmetric.
- A simple example is clipping in a symmetric push-pull amplifier.
- When it is asymmetric, the resulting signal may contain either even or odd harmonics;
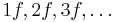
- Simple examples are a half-wave rectifier, and clipping in an asymmetrical class A amplifier.
See also
- Hermitian function for a generalization in complex numbers.
- Taylor series
- Fourier series
- Holstein–Herring method
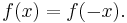
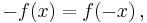
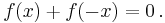
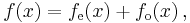
![f_\text{e}(x) = \tfrac12[f(x)%2Bf(-x)]](/2012-wikipedia_en_all_nopic_01_2012/I/397d45d0e49e88cfa73900b4b1961526.png)
![f_\text{o}(x) = \tfrac12[f(x)-f(-x)]](/2012-wikipedia_en_all_nopic_01_2012/I/aa33a0f21f7f54973bd436899747fff2.png)